Page 15 - Semi Conductor use application guide
P. 15
Short-circuit currents
The r.m.s. value of the steady-state short-circuit current which would fl ow in the circuit if there
were no fuse protection is called the prospective current (IEC) or the available short-circuit current
(North America).
In an a.c. circuit, the transient short-circuit current is given by
i = 2I (sin( t + - ) - sin ( - )e - t/tan )
where I is the r.m.s. prospective (available) short-circuit current
is the supply angular frequency ( = 2 f )
is the electrical angle (point on the source voltage wave) at which the short-circuit
begins
-1
is the power-factor angle of the circuit impedance ( = tan L/R)
The fi rst term in the above expression is the steady-state a.c. short-circuit current, while the second
term is an exponentially-decaying transient d.c. component.
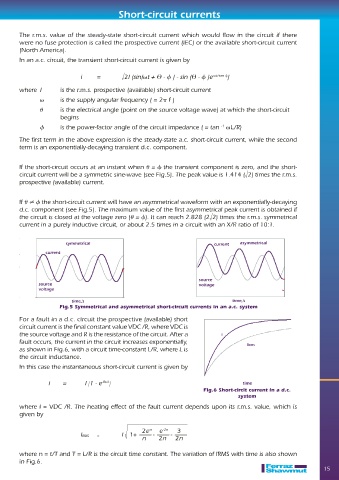
If the short-circuit occurs at an instant when = the transient component is zero, and the short-
circuit current will be a symmetric sine-wave (see Fig.5). The peak value is 1.414 ( 2) times the r.m.s.
prospective (available) current.
If the short-circuit current will have an asymmetrical waveform with an exponentially-decaying
d.c. component (see Fig.5). The maximum value of the fi rst asymmetrical peak current is obtained if
the circuit is closed at the voltage zero ( = ). It can reach 2.828 (2 2) times the r.m.s. symmetrical
current in a purely inductive circuit, or about 2.5 times in a circuit with an X/R ratio of 10:1.
symmetrical current asymmetrical
current
source
source voltage
voltage
time,’s time,’s
Fig.5 Symmetrical and asymmetrical short-circuit currents in an a.c. system
For a fault in a d.c. circuit the prospective (available) short
circuit current is the fi nal constant value VDC /R, where VDC is
the source voltage and R is the resistance of the circuit. After a
fault occurs, the current in the circuit increases exponentially,
as shown in Fig.6, with a circuit time-constant L/R, where L is
the circuit inductance.
In this case the instantaneous short-circuit current is given by
i = I 1 - e -Rt/L
Fig.6 Short-circit current in a d.c.
system
where I = VDC /R. The heating effect of the fault current depends upon its r.m.s. value, which is
given by
-2n
-n
2e e 3
IRMS = I 1+ - - - - -
n 2n 2n
where n = t/T and T = L/R is the circuit time constant. The variation of IRMS with time is also shown
in Fig.6.
15